What Is PI (Maths Is Fun)

Pi (π)

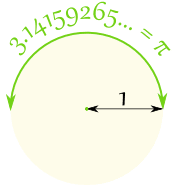Draw a circle with a radius of 1 The distance half way around the circle is 3.14159265... a number known as Pi

Or draw a circle with a diameter (all the way across the circle) of 1 Then the circumference (all the way around the circle) is Pi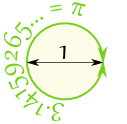

So Pi (the symbol is the Greek letter π) is: The ratio of the Circumference to the Diameter of a Circle.

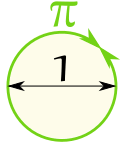
To help you remember what it means
just draw this diagram.

Finding Pi Yourself

Draw a circle, or use something circular like a plate.

Measure around the edge (the circumference):

I got 82 cm

Measure across the circle (the diameter):

I got 26 cm

Divide:

82 cm / 26 cm = 3.1538...

That is pretty close to π. Maybe if I measured more accurately?

Digits

In fact π is approximately equal to:

3.14159265358979323846…

The digits go on and on with no pattern. π has been calculated to over two quadrillion decimal places and still there is no pattern to the digits

Example: You walk around a circle which has a diameter of 100 m, how far have you walked?

Distance walked		= Circumference
		= π × 100 m
		= 314.159... m
		= 314 m (to the nearest m)

Approximation

A quick and easy approximation for π is 22/7

22/7 = 3.1428571...

But as you can see, 22/7 is not exactly right. In fact π is not equal to the ratio of any two numbers, which makes it an irrational number.

A better approximation (but still not exact) is:

355/113 = 3.1415929...
(think "113355", then divide the "355" by the "113")

Remembering The Digits

I usually just remember "3.14159", but you can also count the letters of:

"May I have a large container of butter today"
3 1 4 1 5 9 2 6 5

To 100 Decimal Places

Here is π with the first 100 decimal places:

3.14159265358979323846264338327950288 4197169399375105820974944592307816 4062862089986280348253421170679...

Calculating Pi Yourself

There are many special methods used to calculate π and here is one you can try yourself: it is called the Nilakantha series (after an Indian mathematician who lived in the years 1444–1544).
It goes on for ever and has this pattern:

3 + 42×3×4 − 44×5×6 + 46×7×8 − 48×9×10 + ...

(Notice the + and − pattern, and also the pattern of numbers below the lines.)
It gives these results:

Term	Result (to 12 decimals)
1	3
2	3.166666666667
3	3.133333333333
4	3.145238095238
...	... etc! ...

Get a calculator (or use a spreadsheet) and see if you can get better results.